莫比乌斯反演

莫比乌斯反演

十二月 01, 2021

莫比乌斯反演例题

原理：

技巧：

对于这种与 $\gcd$ 相关的莫比乌斯反演，一般我们都是套路的去设 $f(d)$ 为 $\gcd (i,j)=d$ 的个数，$g(n)$ 为 $\gcd (i,j)=n$ 和 $n$ 的倍数的数的个数

即：

由定义我们容易发现：$f(x)$ 和 $g(x)$ 是有某些关联的，那么我们尝试去发现 $f(x)$ 和 $g(x)$ 的关系，可以发现：

那么此时我们显然就可以运用反演了：

典型例题

P3455 [POI2007]ZAP-Queries

题目描述：

求解：

那么我们设

由反演可知：

我们要求的答案应该是 $f(k)$

那么我们有：

把 $F(d)$ 化简可得：

设 $\lfloor \dfrac d k\rfloor$ 为 $t$

则 $d=kt$ ，所以：

我们根据这个就可以利用整数分块来求了

P2257 YY的GCD

题目描述：

首先我们还是先化简原式：

设：

然后我们把题目写成一般形式就是：

我们要求的答案就是：

我们利用莫比乌斯反演，即上面的第三个式子就有：

我们设 $\lfloor \dfrac d p\rfloor = t$ 则 $d=pt$

现在我们是枚举每一个 $p$ 的倍数进行处理，因此我们也可以改成枚举每一个数的质因数

把 $\lfloor \dfrac m i \rfloor \lfloor \dfrac n i\rfloor $ 扔出来就有：

我们观察发现：后面的 $\sum \mu (\dfrac i t)$ 可以直接处理掉

当然，在我们也可以根据一些代数意义化简，当我们化简到这一步的时候：

翻译成人话就是：对于每一个质数，我枚举它的倍数，使得 $ans$ 加上 $\mu(\lfloor\dfrac d p \rfloor) F(d)$

那么我们完全可以换一种思路，枚举每一个数，加上它分解质因数后的每一个因数即可，此时对于我的 $\mu$ 来说，就是 $i$ 是 $p$ 的多少倍，$F$ 就是当前的 $i$ 是几

然后拆开 $F(i)$ 就行了

其实和上面的化简是长的一样的，只是换一种理解方式，可以减少很多不必要的步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<cctype>
#include<bitset>
#include<vector>
#include<map>
#include<set>
#define int long long
using namespace std;
const int N=1e7+5e5+5;
const int mod=1e9+7;
const double pi=3.141592653589793;
typedef long long ll;
typedef pair<int,int> P;
namespace scan{
    template <typename T>
    void read(T &x){
        x=0; char c=getchar(); int f=0;
        for(; !isdigit(c); c=getchar()) f |= c=='-';
        for(; isdigit(c); c=getchar()) x = x*10+(c^48);
        if(f) x = -x;
    }

    template <typename T>
    void write(T &x,char ch){
        if(x<0) putchar('-'), x = -x;
        static short st[30],tp;
        do st[++tp] = x%10, x/=10; while(x);
        while(tp) putchar(st[tp--] | 48);
        putchar(ch);
    }
}
using namespace scan;
int n,m,cnt;
int prime[N],mu[N],g[N];
int sum[N];
bool st[N];
inline void get_prime(int n){
	mu[1]=1;
	for(int i=2;i<n;i++){
		if(!st[i]) prime[++cnt]=i,mu[i]=-1;
		for(int j=1;prime[j]*i<n;j++){
			st[i*prime[j]]=true;
			if(i%prime[j]==0) break ;
			mu[i*prime[j]]=-mu[i];
		}
	}
	for(int j=1;j<=cnt;j++)
		for(int i=1;i*prime[j]<=n;i++) g[i*prime[j]]+=mu[i];
	for(int i=1;i<=n;i++) sum[i]=sum[i-1]+g[i];
}
int T,ans;
signed main(){
	get_prime(N-100);
	// for(int i=1;i<=cnt;i++) cout<<prime[i]<<" ";
	read(T);
	while(T--){
		ans=0;
		read(n),read(m);
		for(int l=1,r;l<=n;l=r+1){
			if(n/l==0 || m/l==0) break;
			r=min(n/(n/l),(m/(m/l)));
			ans+=(sum[r]-sum[l-1])*(m/l)*(n/l);
		}
		write(ans,'\n');
	}
    return 0;
}
P3327 [SDOI2015]约数个数和

题目描述：

首先有一个引理：

找了半天也没找到证明，貌似只有一个，还是我没看懂的

所以我们就直接搞吧

于是我们直接设

反演一下：

于是有：

我们的答案是 $f(1)$

所以

我们发现前面的 $\mu$ 可以前缀和预处理掉显然好处理，后面的我们可以考虑想想办法

我们尝试先把后面的 $d$ 扔出去

我们这时候发现 $\lfloor \dfrac n {di} \rfloor$ 与 $j$ 无关，可以放到前面：

我们发现后面的两个 $\Sigma$ 互不影响

这样，我们就可以分别处理了，时间复杂度 $O(T\sqrt n +n\sqrt n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<cctype>
#include<bitset>
#include<vector>
#include<map>
#include<set>
using namespace std;
using ll=long long;
const int N=5e4+5;
const int mod=1e9+7;
const double pi=3.141592653589793;
typedef long long ll;
typedef pair<int,int> P;

namespace scan{
    template <typename T>
    void read(T &x){
        x=0; char c=getchar(); int f=0;
        for(; !isdigit(c); c=getchar()) f |= c=='-';
        for(; isdigit(c); c=getchar()) x = x*10+(c^48);
        if(f) x = -x;
    }

    template <typename T>
    void write(T x,char ch){
        if(x<0) putchar('-'), x = -x;
        static short st[30],tp;
        do st[++tp] = x%10, x/=10; while(x);
        while(tp) putchar(st[tp--] | 48);
        putchar(ch);
    }
}
using namespace scan;
int n,m,T;
int mu[N];
long long sum[N],h[N];
inline void get_mu(int n){
	mu[1]=1;
	for(int i=1;i<=n;i++)
		for(int j=i+i;j<=n;j+=i) mu[j]-=mu[i];
	for(int i=1;i<=n;i++) sum[i]=sum[i-1]+mu[i];
	for(int d=1;d<=n;d++){
		ll res=0;
		for(int l=1,r;l<=d;l=r+1){
			r=d/(d/l);
			res+=1ll*(r-l+1)*1ll*(d/l);
		}
		h[d]=res;
	}//n sqrt n
}
int main(){
    get_mu(N-5);
    // for(int i=1;i<=100;i++) cout<<h[i]<<" ";
    // cout<<endl;
	read(T);
	while(T--){
    	read(n),read(m);
    	if(n>m) swap(n,m);
    	ll ans=0;
    	for(int l=1,r;l<=n;l=r+1){
    		r=min(n/(n/l),m/(m/l));
    		// cout<<l<<" "<<r<<" ";
    		ans+=1ll*(sum[r]-sum[l-1])*1ll*h[n/l]*h[m/l];
    	}
    	write(ans,'\n');
	}
    return 0;
}
P1829 [国家集训队]Crash的数字表格 / JZPTAB

题目描述：

数据范围：$1\le n,m\le 10^7$

首先我们根据小学知识可以发现

$\gcd(i,j)*\mathrm{lcm}(i,j)=i\times j$

所以我们的题意就变成了

那么就好做多了，我们可以直接枚举 $\gcd $ 并把它放到最前面

我们枚举 $d$ 的倍数可以发现：

我们把 $\mu (k)$ 的枚举项拿出来，那么式子就变成了（为了方便，就不写 $\min$ 了）

我们这个式子的最后一个 $\sum$ 的意思是，从 $1\sim \dfrac n d$ 中选取 $k$ 的倍数相加，那么我们可以直接写成：

最后两个 $\sum$ 很明显示两个等差数列，我们兴奋地写成等差数列形式

然后我们先枚举后面巨大的等差数列求和就有：

那么后面就可以分别预处理加整除分块来做了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
/*
BlackPink is the Revolution
light up the sky
Blackpink in your area
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<cctype>
#include<bitset>
#include<vector>
#include<map>
#include<set>
using namespace std;
using ll=long long;
const int N=1e7+5;
const int mod=20101009;
const double pi=3.141592653589793;
typedef pair<int,int> P;

namespace scan{
    template <typename T>
    void read(T &x){
        x=0; char c=getchar(); int f=0;
        for(; !isdigit(c); c=getchar()) f |= c=='-';
        for(; isdigit(c); c=getchar()) x = x*10+(c^48);
        if(f) x = -x;
    }

    template <typename T>
    void write(T x,char ch){
        if(x<0) putchar('-'), x = -x;
        static short st[30],tp;
        do st[++tp] = x%10, x/=10; while(x);
        while(tp) putchar(st[tp--] | 48);
        putchar(ch);
    }
}
using namespace scan;
int mu[N],prime[N],cnt;
ll sum[N],h[N];
bool st[N];
template<typename T>
inline int qm(T a){
	return (a%mod+mod)%mod;
}

inline int add(int a,int b){
	return (a+b)%mod;
}

inline void get_prime(int n){
	mu[1]=1;
	for(int i=2;i<n;i++){
		if(!st[i]) prime[++cnt]=i,mu[i]=-1;
		for(int j=1;prime[j]*i<n;j++){
			st[i*prime[j]]=true;
			if(i%prime[j]==0) break ;
			mu[i*prime[j]]=-mu[i];
		}
	}
	for(int i=1;i<=n;i++) mu[i]=qm(1ll*mu[i]*i*i);
	for(int i=1;i<=n;i++) sum[i]=add(sum[i-1],mu[i]);
}

inline int get_sum(int x,int y){
	return qm(1ll*qm(1ll*x*(x+1)/2)*qm(1ll*y*(y+1)/2));
}

inline int g(int x,int y){
	if(x>y) swap(x,y);
	ll res=0;
	for(int l=1,r;l<=x;l=r+1){
		r=min(x/(x/l),y/(y/l));
		res=add(res, qm(1ll*(sum[r]-sum[l-1])*(get_sum(x/l,y/l))));
	}
	return res%mod;
}

int n,m;
ll res=0;
int main(){
	get_prime(N);
    read(n),read(m);
    if(n>m) swap(n,m);
    for(int l=1,r;l<=n;l=r+1){
    	r=min(n/(n/l), m/(m/l));
    	res=add(res, qm(1ll*(r-l+1)*(l+r)/2%mod*g(n/l,m/l)));
    }
    write(qm(res),'\n');
    return 0;
}
AT5200 [AGC038C] LCMs

题目描述：

首先，利用容斥原理我们会发现，上面的这个玩意长成这样肯定不想要的

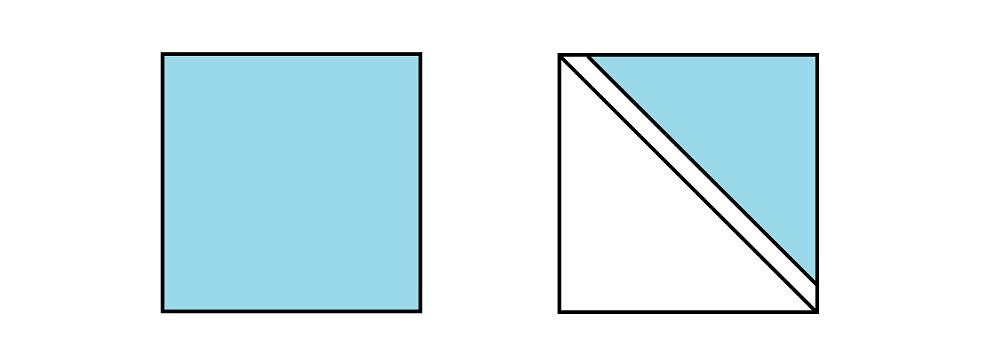
于是我们把它们放到一个按 $A_1 ~A_2~A_3~A_4~A_5~A_6\dots A_n$ 上

很容易发现，我们要求的就是右边的那个大三角，

但是我们发现肯定是左边的更好处理，所以我们可以开始行动了

那我们就只把那一块拿出来观察：

然后我们就能进行反演了：

后面的应该可以开个桶来处理了

然后我们直接枚举桶里面的元素即可